Exam tactics

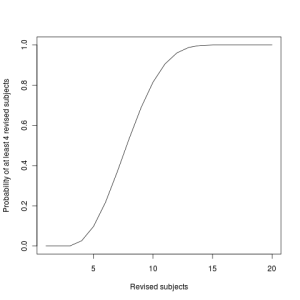
Say you have 20 essay topics. You know that there will be 9 exam questions and you’ll be expected to answer 4 questions. How many topics ought you revise? The simplest answer is 15. If you study 15 topics, even if all 5 topics you didn’t study get picked, there’ll be 4 left that you did study (because 9 get picked, remember). But that’s still a lot of topics! If you studied 14 topics, what are the odds that you’d only have 3 revised topics on the exam?

The answer is “Use the hypergeometric distribution, Luke”. The idea is to imagine each topic is a ball in an urn. The examiner draws 9 balls from the urn without replacement. Some balls are white (revised) some are black (not revised). The relevant question is, “what is the probability of 3 or fewer white balls on the assumption that there are N out of 20 white balls in the urn? For N=14, it turns out that your chance of not getting 4 revised questions is about 0.2%. Or one in five hundred. I like those odds. For N=13 it’s about 1% and for N=12 it’s about 3%. Is that an acceptable risk? For N=11 we’re up to 9%, almost one in ten.

I am of course, making plenty of assumptions here. For example, I’m assuming revision is a binary choice. It’s a yes/no question whether you revise any given topic. You can of course choose to invest more or less time revising each topic and this will affect your grade. One hopes that exam grade is a strictly increasing function of time spent revising, but I expect its second derivative is negative: the more time you spend revising, the less extra revision will improve your mark. It’s probably roughly logarithmic. Money has diminishing marginal utility: the more money you have, the less you value more money. Exam revision works the same way, probably.

There’s also the question of revision time affecting marks on topics in the same way. It’s likely you’ll find some topics easier than others, and that time invested revising them will more rapidly increase your potential mark (although that will still tail off logarithmically…).

I am also assuming that every topic is equally likely to come up. You might be able to make educated guesses about which topics are more or less likely.

Once we add in those factors, we probably have a very interesting optimisation problem. I’m going to go and play with R‘s hypergeometric functions some more! Here is a graph, so you know what I’m saying is true.